Theory of GNNs 2 - Machine Learning with Graphs

Counting Cycle Lengths with GNNs¶

In the lecture, we listed the following observaitons about a perfect GNN:

Observation 1: If two nodes have the same neighborhood structure, they must have the same embedding.
Observation 2: If two nodes have different neighborhood structure, they must have different embeddings.

Considering observation 2, we stated that message-passing GNNs cannot count the cycle length, and we showed the following example with cycle lengths of 3 and 4.

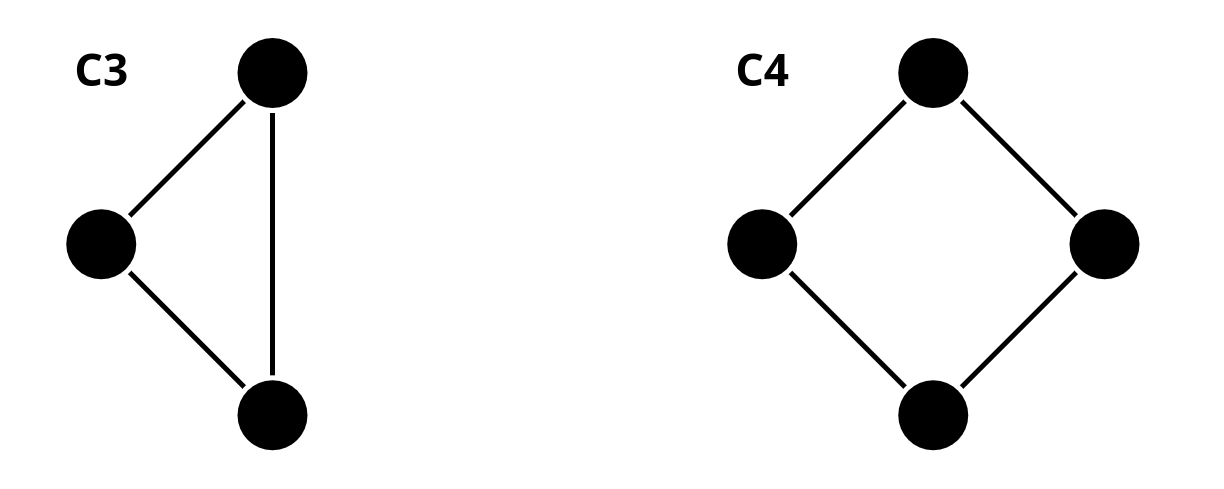
What’s the reason that a message-passing based GNN cannot distinguish $C3$ and $C4$ ? Is this true for any $Ci$ and $Cj$ where $i,j \geq 3$ ?

Let’s verify this using PyG. The following code snippet involves a simple GNN with GCN layers and a global pooling to get graph-level representations. Play with the parameters (e.g., number of layers, dimensions) to check if our statement holds.

import torch
import torch.nn.functional as F
from torch_geometric.data import Data
from torch_geometric.nn import GCNConv
from torch_geometric.nn.pool import global_mean_pool

class SimpleGCN(torch.nn.Module):
    def __init__(self, hidden_dim=8):
        super().__init__()
        self.conv1 = GCNConv(1, hidden_dim)
        self.conv2 = GCNConv(hidden_dim, hidden_dim)

    def forward(self, x, edge_index, batch):
        x = F.relu(self.conv1(x, edge_index))
        x = F.relu(self.conv2(x, edge_index))
        return global_mean_pool(x, batch)

# C3
edge_index_C3 = torch.tensor([
    [0,1, 1,2, 2,0],
    [1,0, 2,1, 0,2]
], dtype=torch.long)
x_C3 = torch.ones((3,1))
data_C3 = Data(x=x_C3, edge_index=edge_index_C3)

# C4
edge_index_C4 = torch.tensor([
    [0,1, 1,2, 2,3, 3,0],
    [1,0, 2,1, 3,2, 0,3]
], dtype=torch.long)
x_C4 = torch.ones((4,1))
data_C4 = Data(x=x_C4, edge_index=edge_index_C4)

# run the model
model = SimpleGCN()
with torch.no_grad():
    out_C3_mean = model(data_C3.x, data_C3.edge_index, data_C3.batch)
    out_C4_mean = model(data_C4.x, data_C4.edge_index, data_C4.batch)

print("C3:", out_C3_mean)
print("C4:", out_C4_mean)

C3: tensor([[0.5712, 0.3294, 0.1356, 0.2964, 0.0000, 0.0000, 0.4536, 0.0512]])
C4: tensor([[0.5712, 0.3294, 0.1356, 0.2964, 0.0000, 0.0000, 0.4536, 0.0512]])

What if we used global sum pooling instead of mean? Edit the code snippet and test if the embeddings differ.

What about the following graphs? Can sum pooling distinguish them? Run the following code snippet and play with parameters to formulate your answer.

import torch
import torch.nn.functional as F
from torch_geometric.data import Data
from torch_geometric.nn import GCNConv
from torch_geometric.nn.pool import global_add_pool

class SimpleGCN(torch.nn.Module):
    def __init__(self, hidden_dim=8):
        super().__init__()
        self.conv1 = GCNConv(1, hidden_dim)
        self.conv2 = GCNConv(hidden_dim, hidden_dim)

    def forward(self, x, edge_index, batch):
        x = F.relu(self.conv1(x, edge_index))
        x = F.relu(self.conv2(x, edge_index))
        return global_add_pool(x, batch)

# C6
edge_index_C6 = torch.tensor([
    [0, 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 0],
    [1, 2, 3, 4, 5, 0, 0, 1, 2, 3, 4, 5]
], dtype=torch.long)
x_C6 = torch.ones((6, 1))  # initial features all identical
data_C6 = Data(x=x_C6, edge_index=edge_index_C6)

# Two triangles (C3 + C3)
edge_index_C3C3 = torch.tensor([
    [0,1,2, 3,4,5, 1,2,0, 4,5,3],
    [1,2,0, 4,5,3, 0,1,2, 3,4,5]
], dtype=torch.long)
x_C3C3 = torch.ones((6, 1))  # same shape as C6
data_C3C3 = Data(x=x_C3C3, edge_index=edge_index_C3C3)

# run the model
model = SimpleGCN()
with torch.no_grad():
    out_C6 = model(data_C6.x, data_C6.edge_index, data_C6.batch)
    out_C3C3 = model(data_C3C3.x, data_C3C3.edge_index, data_C3C3.batch)

print("C6:", out_C6)
print("C3C3:", out_C3C3)

C6: tensor([[0.0100, 0.0000, 0.4739, 0.0000, 1.2981, 1.0449, 0.7568, 0.0000]])
C3C3: tensor([[0.0100, 0.0000, 0.4739, 0.0000, 1.2981, 1.0449, 0.7568, 0.0000]])

Interpret your findings about how good are message-passing based GNNs on counting cycle lengths. What’s the effect of global sum pooling and does sum pooling solve the issue?

Positional Awareness in GNNs¶

Consider the following path graph $G$ where all node features are zero.

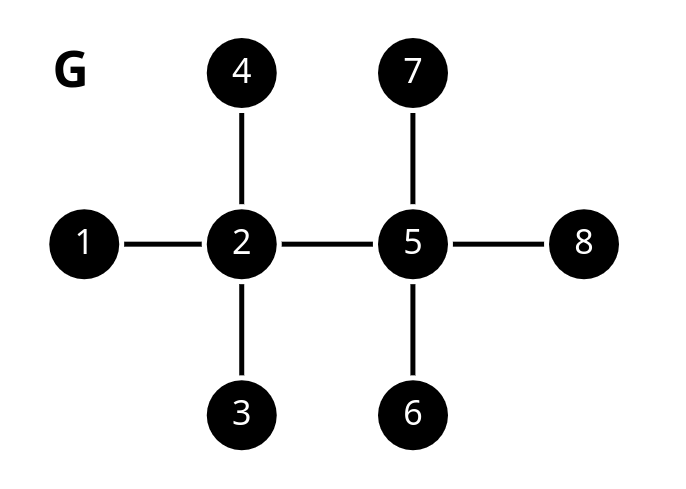
Answer briefly:

Can any message passing GNN distinguish nodes 2 and 5, why? (Hint: You can compare their computation graphs.)

Now, let’s pick node 1 as an anchor node. We do this by defining a new feature for each node as follows:
$d_1(v) = \text{dist}(v, \text{anchor node }1)$
(1)
Compute new (initial) node features that include $d_1(v)$ .

Can nodes 2 and 5 be identified now? What about 3 and 4?

How many anchors do we need and which nodes to select as anchors to distinguish all nodes?

When We Really Want to Count Cycles¶

Let’s revisit the cycle counting problem. A recent paper from ICLR 2024 (link) proposes Moment-GNN and shows that if we feed random node features (IDs) and use a simple sum‑aggregation GNN + a polynomial nonlinearity (“moment” layer), then the resulting graph embedding encodes statistics that correlate with substructure counts (e.g., counts of closed walks, which relate to cycles).

We’ll test the following graphs:

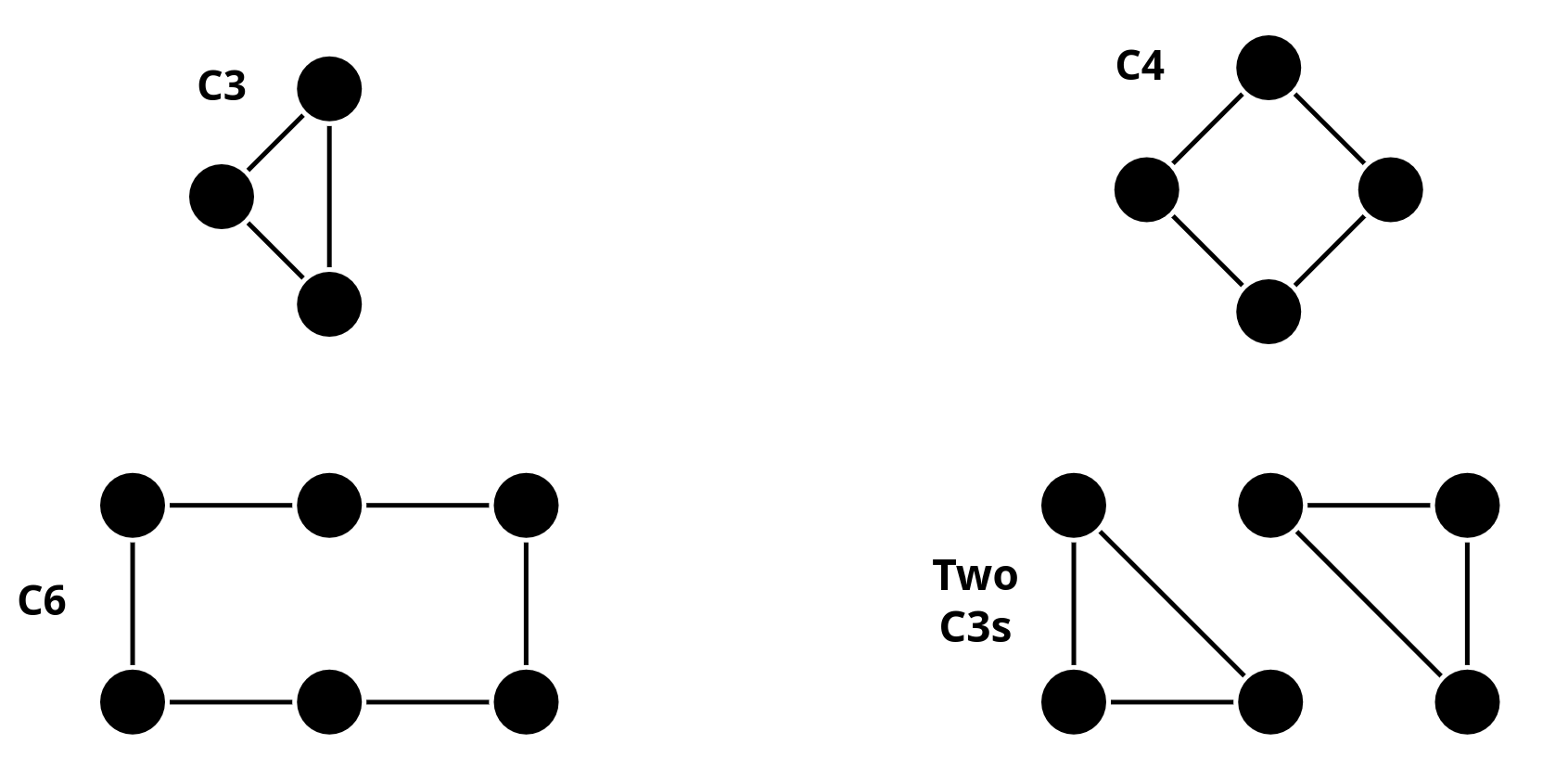
In the following code snippet, we reuse the graphs definitions we used so far. Also, we have a simplified MomentGNN implementation.

Notice that we still have the idential initial node features for all graphs.

Tasks:

Run the MomentGNN with identical initial node features and interpret the output. Can it distinguish the graphs?

import torch
from torch_geometric.data import Data
from torch_geometric.utils import scatter

# C3
edge_index_C3 = torch.tensor([
    [0,1, 1,2, 2,0],
    [1,0, 2,1, 0,2]
], dtype=torch.long)
x_C3 = torch.ones((3, 1))  # initial features all identical
data_C3 = Data(x=x_C3, edge_index=edge_index_C3)

# C4
edge_index_C4 = torch.tensor([
    [0,1, 1,2, 2,3, 3,0],
    [1,0, 2,1, 3,2, 0,3]
], dtype=torch.long)
x_C4 = torch.ones((4, 1))  # initial features all identical
data_C4 = Data(x=x_C4, edge_index=edge_index_C4)

# C6
edge_index_C6 = torch.tensor([
    [0, 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 0],
    [1, 2, 3, 4, 5, 0, 0, 1, 2, 3, 4, 5]
], dtype=torch.long)
x_C6 = torch.ones((6, 1))  # initial features all identical
data_C6 = Data(x=x_C6, edge_index=edge_index_C6)

# Two triangles (C3 + C3)
edge_index_C3C3 = torch.tensor([
    [0,1,2, 3,4,5, 1,2,0, 4,5,3],
    [1,2,0, 4,5,3, 0,1,2, 3,4,5]
], dtype=torch.long)
x_C3C3 = torch.ones((6, 1))  # initial features all identical
data_C3C3 = Data(x=x_C3C3, edge_index=edge_index_C3C3)

def moment_gnn_stat(data):
    x = data.x
    edge_index = data.edge_index

    # aggregate incoming messages from neighbors using sum
    agg = scatter(
        x[edge_index[0]], # source node features
        edge_index[1], # index of target nodes
        dim=0,
        dim_size=x.size(0),
        reduce='sum'
    )

    # add the aggregated messages to the original features
    h1 = x + agg

    # element-wise square
    h2 = h1 * h1

    # sum pooling
    g = h2.sum(dim=0)

    # return the L2 norm of the graph representation
    return torch.norm(g).item()

# Run experiments
graphs = {
    "C3": data_C3,
    "C4": data_C4,
    "two_C3": data_C3C3,
    "C6": data_C6
}

for name, G in graphs.items():
    print(name, moment_gnn_stat(G))

Edit the code snippet so node features are random $d$ -dimensional vectors. Try different values of $d$ and interpret your results. Are the final embeddings of all graphs different?