Trees and Forests

Trees and Forests#

Building a simple Decision Tree Classifier!

Author: Bjarne C. Hiller

Hide code cell content 
import numpy as np
import pandas as pd

from sklearn.base import BaseEstimator, ClassifierMixin
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

Ingredients#

  • np.unique and np.unique_counts

  • np.argmax

Implementation#

Let’s start with a simple class to hold the decision rules associated with each tree node. Each decision rule splits the data by comparing one of the features against a threshold value.

class TreeNode:
    """Represents one split in the Decision Tree."""

    def __init__(self, feature=None, value=None):
        self.left = None
        self.right = None
        self.feature = feature
        self.value = value
        self.samples = None
    
    def split(self, X):
        left = X[..., self.feature] < self.value
        return left, ~left
    
    def is_leaf(self):
        """Is this a leaf node?"""
        return (self.left is None) and (self.right is None)

    def __repr__(self):
        if self.is_leaf():
            return f"TreeNode({self.samples})"
        return f"TreeNode({self.samples}, {self.feature} < {self.value:.2f})"

Next, we will write a class that generates split candidates. One of the simplest approaches is to use the median of each feature as split value:

class Splitter:

    def make_splits(self, X, y) -> list[TreeNode]:
        """Generates candidate splits."""
        pass

class MedianSplitter(Splitter):
    """Generates splits by using the Median for each feature."""

    def make_splits(self, X, y) -> list[TreeNode]:
        n, p = X.shape
        splits = []
        medians = np.median(X, axis=0)
        for i in range(p):
            node = TreeNode(feature=i, value=medians[i])
            splits.append(node)
        return splits

Now, we need some criterion to evaluate the generated splits and pick the best candidate:

class Criterion:
    def evaluate(self, X, y, split: TreeNode):
        pass

    def __call__(self, X, y, split: TreeNode):
        return self.evaluate(X, y, split)

The Gini index, named after the mathematician Corrado Gini, is a measure of class impurity, that the Decision Tree tries to minimize. It represents, of how often a randomly chosen instance would be incorrectly labeled, if labels were decided randomly according to the relative number of instances of the respective class.

Let \(Y\) be a multiset of class labels from the underlying class set \(C=\{1, ..., c\}\). Then the relative frequencies \(p_i\) of each class \(i\in C\) is given by:

\[ p_i = \frac{|\{y \in Y | y=i\}|}{|Y|} \]

Then, the gini index \(I_G\) can be computed as:

\[\begin{split} \begin{align*} I_G(p) &= \sum_{i=1}^c \left( p_i \sum_{j \neq i} p_j \right)\\ &= \sum_{i=1}^c p_i (1 - p_i)\\ &= \sum_{i=1}^c (p_i - p_i^2)\\ &= \sum_{i=1}^c p_i - \sum_{i=1}^c p_i^2\\ &= 1 - \sum_{i=1}^c p_i^2 \end{align*} \end{split}\]

A gini index of 0 means, that all instances belong to the same class.

def gini_index(labels) -> float:
    """Computes the Gini-Index for a given numpy array of labels."""
    gini = 0
    # TODO: Implement computation of the Gini-Index!
    return gini
Hide code cell content 
def gini_index(labels) -> float:
    """Computes the Gini-Index for a given numpy array of labels."""
    _, counts = np.unique_counts(labels)
    p = counts / counts.sum()
    return 1 - np.power(p, 2).sum()

assert gini_index([0,0,0]) == 0
assert gini_index([0,1]) == 0.5

class GiniCriterion(Criterion):
    """Evaluates splits using the gini index."""
 
    def evaluate(self, X, y, split: TreeNode):
        left, right = split.split(X)
        gini = gini_index(y)
        gini_left = 0
        if len(y[left]) > 0:
            gini_left = len(y[left]) / len(y) * gini_index(y[left])
        gini_right = 0
        if len(y[right]) > 0:
            gini_right = len(y[right]) / len(y) * gini_index(y[right])
        return gini - gini_left - gini_right

Finally, we will bring everything together in this Tree class. At each node, the tree will generate new candidate splits with the Splitter object, evaluate them with the criterion, and use the best candidate to split the data into a left and a right child node. This will continue, until all samples belong to the same class or the maximum depth is reached:

class Tree(BaseEstimator, ClassifierMixin):
    def __init__(self, max_depth=None, criterion="gini", splitter="median"):
        super().__init__()
        self.max_depth = max_depth
        self.root_ = None
        self.classes_ = None
        self.criterion = criterion
        if self.criterion == "gini":
            self.criterion = GiniCriterion()
        self.splitter = splitter
        if self.splitter == "median":
            self.splitter = MedianSplitter()
    
    def fit(self, X, y):
        # save class labels observed in training data
        self.classes_ = np.unique(y)

        # recursively grow tree and return root node
        self.root_ = self.grow(X, y, 1)

    def class_counts(self, y):
        """Helper function to receive class counts."""
        bins = np.zeros_like(self.classes_)
        for i, c in enumerate(self.classes_):
            bins[i] = np.sum(y == c)        
        return bins
    
    def grow(self, X, y, depth):
        """Recursively grow a tree."""
        n, p = X.shape
        samples = self.class_counts(y)

        # return leaf node
        if len(np.unique(y)) <= 1 or (self.max_depth is not None and depth >= self.max_depth):
            leaf = TreeNode()
            leaf.samples = samples
            return leaf

        # generate splits
        splits = self.splitter.make_splits(X, y)

        # evaluate splits and aggregate scores
        scores = [self.criterion.evaluate(X, y, split) for split in splits]       

        # gest best split
        node = splits[np.argmax(scores)]
        node.samples = samples
        left, right = node.split(X)

        # check for degenerate splits
        if len(y[left]) == 0 or len(y[left]) == 0:
            leaf = TreeNode()
            leaf.samples = samples
            return leaf

        # grow left and right children
        node.left = self.grow(X[left], y[left], depth+1)
        node.right = self.grow(X[right], y[right], depth+1)
        return node
    
    def traverse(self, x) -> TreeNode:
        node = self.root_
        while not node.is_leaf():
            left, right = node.split(x)
            if left.all():
                node = node.left
            else:
                node = node.right
        return node

    def predict(self, X):
        predictions = []
        for x in X:
            # get leaf nod
            leaf = self.traverse(x)
            main_class = np.argmax(leaf.samples)
            y = self.classes_[main_class]
            predictions.append(y)
        return predictions

    def __str__(self):
        text = ""
        nodes = [self.root_]
        while nodes:
            text += "\t".join([str(n) for n in nodes]) + "\n"
            nodes = sum([[n.left, n.right] for n in nodes], start=[])
            nodes = [n for n in nodes if n is not None]
        return text

Test on Iris Dataset#

Let’s try out our implementation on the iris dataset:

iris_ds = load_iris()

# only use petal length and petal width
X = iris_ds["data"][:, [2,3]]
y = iris_ds["target"]

X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.8, random_state=19)

tree = Tree()
tree.fit(X_train, y_train)

tree.root_

TreeNode([40 38 42], 0 < 4.45)

from sklearn.metrics import accuracy_score

y_pred = tree.predict(X_test)

acc = accuracy_score(y_test, y_pred)

print(f"Test Accuracy: {acc:.2f} %")

Test Accuracy: 0.97 %

tree

TreeNode([40 38 42], 0 < 4.45)
TreeNode([40 20  0], 0 < 1.55)	TreeNode([ 0 18 42], 1 < 1.80)
TreeNode([30  0  0])	TreeNode([10 20  0], 1 < 1.00)	TreeNode([ 0 17  4], 1 < 1.50)	TreeNode([ 0  1 38], 1 < 2.00)
TreeNode([10  0  0])	TreeNode([ 0 20  0])	TreeNode([0 5 0])	TreeNode([ 0 12  4], 0 < 4.65)	TreeNode([ 0  1 14], 0 < 5.10)	TreeNode([ 0  0 24])
TreeNode([0 7 1])	TreeNode([0 5 3], 0 < 5.00)	TreeNode([0 1 5], 0 < 4.85)	TreeNode([0 0 9])
TreeNode([0 3 0])	TreeNode([0 2 3], 1 < 1.60)	TreeNode([0 1 2])	TreeNode([0 0 3])
TreeNode([0 0 2])	TreeNode([0 2 1], 0 < 5.10)
TreeNode([0 1 0])	TreeNode([0 1 1], 0 < 5.45)
TreeNode([0 1 0])	TreeNode([0 0 1])
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
from sklearn.inspection import DecisionBoundaryDisplay
import matplotlib.pyplot as plt

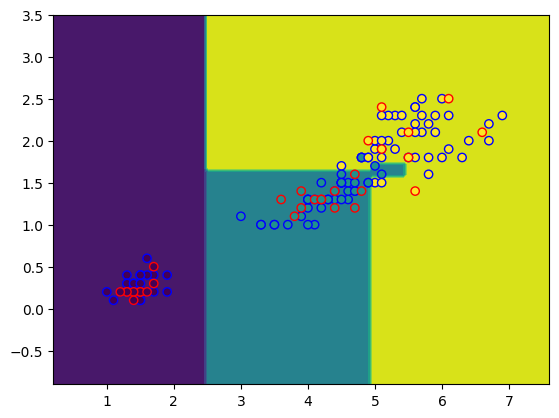
DecisionBoundaryDisplay.from_estimator(tree, X_test)
plt.scatter(X_train[:,0], X_train[:,1], c=y_train, edgecolors="b")
plt.scatter(X_test[:,0], X_test[:,1], c=y_test, edgecolors="r");
_images/542f3deee9eca86f745448d55d25dd37d54740599dd7dce68b6ec984654a42ee.png

Outlook#

Fortunately, sklearn already provides an implementation via the DecisionTreeClassifier and DecisionTreeRegressor

from sklearn.tree import DecisionTreeClassifier, DecisionTreeRegressor, plot_tree

model = DecisionTreeClassifier()

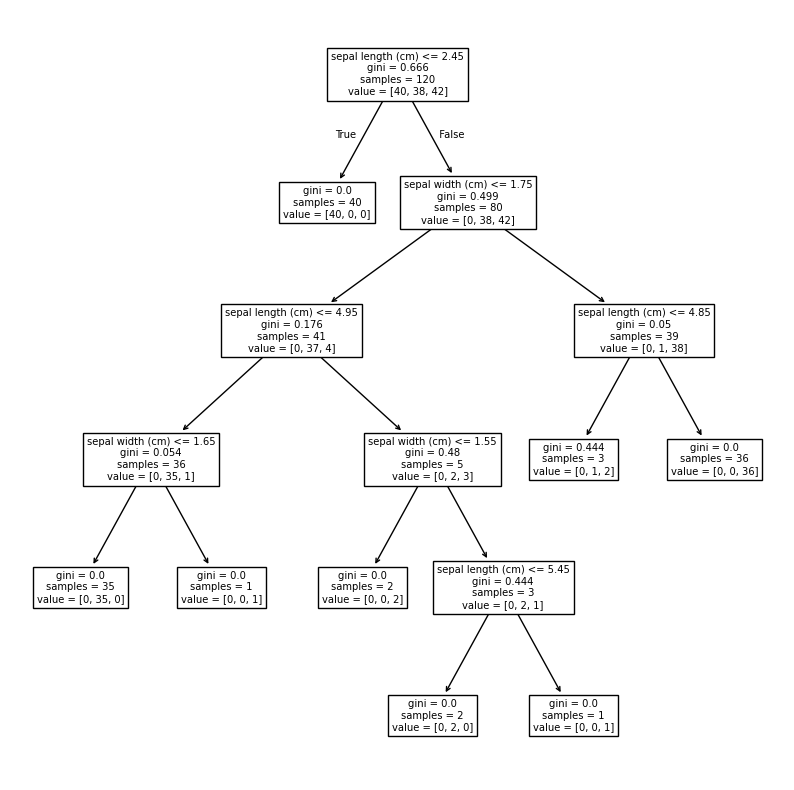
fig, ax = plt.subplots(figsize=(10,10))
model.fit(X_train, y_train)
plot_tree(model, feature_names=iris_ds["feature_names"], ax=ax);
_images/6ca2184cb56f9446513d6759294fbeb1f969d4df23813d8fd6796ae076226f0b.png 
fig, ax = plt.subplots()
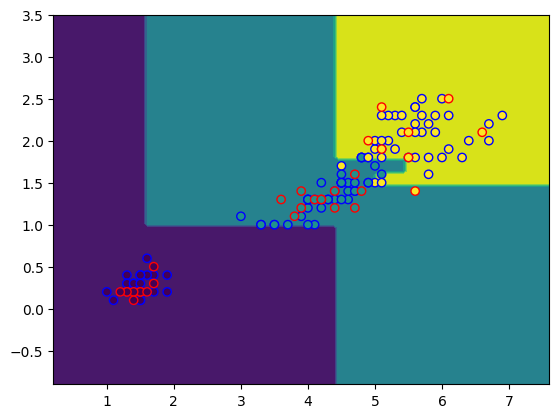
DecisionBoundaryDisplay.from_estimator(model, X_test, ax=ax)

plt.scatter(X_train[:,0], X_train[:,1], c=y_train, edgecolors="b")
plt.scatter(X_test[:,0], X_test[:,1], c=y_test, edgecolors="r");
_images/2a307a8b4078835b514f5246545e81ab2396f802413c3545c5bd38c382a79705.png
Contents