Manual Model Evaluation¶
The following tasks require you to do the training and prediction of some models by hand. So grab a piece of paper, your favorite notetaking app or simply a text editor and paint. This concerns the tasks before the data generation part.
Data¶
Training Data¶
| x1 | x2 | y |
|---|---|---|
| 0 | 0 | -1 |
| 0 | 1 | -1 |
| 1 | 1 | -1 |
| 1 | 0 | 1 |
Test Data¶
| x1 | x2 | y |
|---|---|---|
| 0 | 0.1 | -1 |
| 1 | 0.1 | -1 |
Model¶
Your answer
Example Data¶
Let’s look at how such models behave when there is more data. No need to work through all the tasks exclusively by hand from here on.
Generate “Perfect” Data Points with Values in .¶
import numpy as np
import matplotlib.pyplot as plt
X_raw = np.random.uniform(0, 1, (1000, 2))Source
# plot
plt.scatter(X_raw[:, 0], X_raw[:, 1], s=10)
plt.title("Raw Data Points")
plt.xlabel("x1")
plt.ylabel("x2")
plt.xlim(-0.25, 1.25)
plt.ylim(-0.25, 1.25)
plt.gca().set_aspect("equal")
plt.legend(["Raw Points"])
plt.show()
Add Ground Truth Class Labels from Underlying Separating Line¶
Y = np.array([np.sign(x2 - x1) if np.sign(x2 - x1) != 0 else 1 for x1, x2 in X_raw])Source
# plot
plt.scatter(X_raw[Y == -1][:, 0], X_raw[Y == -1][:, 1], s=10, c="Red")
plt.scatter(X_raw[Y == 1][:, 0], X_raw[Y == 1][:, 1], s=10, c="Blue")
plt.title("Raw Data Points with Labels")
plt.xlabel("x1")
plt.ylabel("x2")
plt.xlim(-0.25, 1.25)
plt.ylim(-0.25, 1.25)
plt.gca().set_aspect("equal")
plt.plot([-1, 2], [-1, 2], c="Gray")
plt.legend(["Raw Points of Class -1", "Raw Points of Class 1", "Actual Class Border"])
plt.show()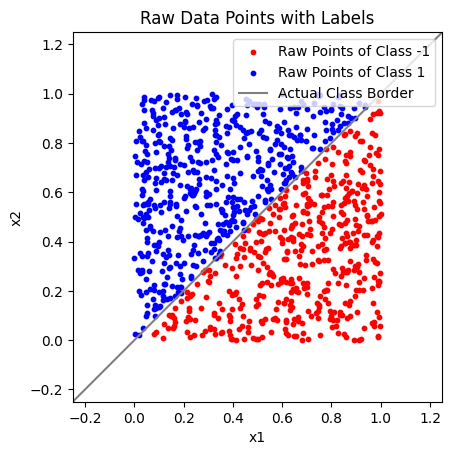
Add Random Noise to the Data Points¶
X = X_raw + np.random.normal(0, 0.1, (1000, 2))Source
# plot
plt.scatter(X[Y == -1][:, 0], X[Y == -1][:, 1], s=10, c="Red")
plt.scatter(X[Y == 1][:, 0], X[Y == 1][:, 1], s=10, c="Blue")
plt.title("Noisy Data Points with Labels")
plt.xlabel("x1")
plt.ylabel("x2")
plt.xlim(-0.25, 1.25)
plt.ylim(-0.25, 1.25)
plt.gca().set_aspect("equal")
plt.plot([-1, 2], [-1, 2], c="Gray")
plt.legend(["Noisy Points of Class -1", "Noisy Points of Class 1", "Best Classification Border"])
plt.show()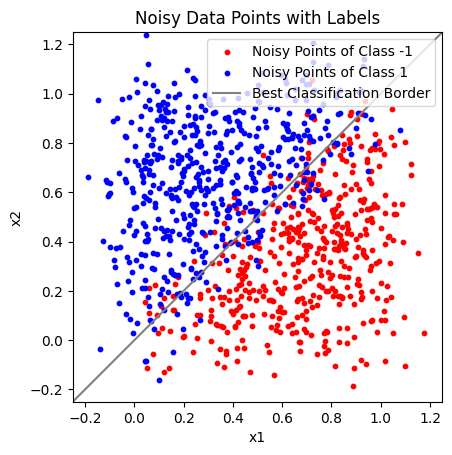
The “Best Classification Border” is the same line as the “Actual Class Border” before. Because we added normally distributed noise to the data points, this is the theoretically optimal line to distinguish between class -1 and 1.
Note that even this model is not entirely free of errors.
Decision Tree Classifier¶
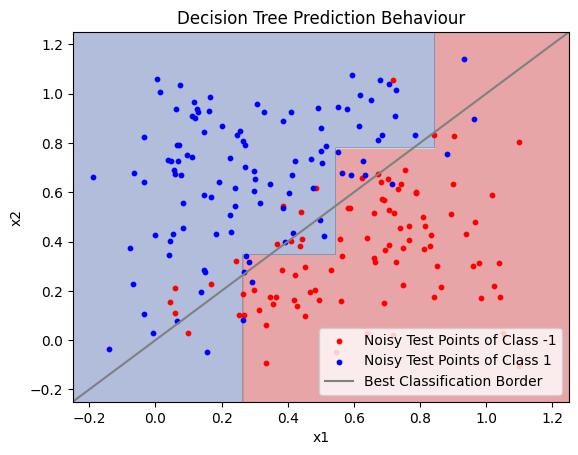
You can see how a decision tree classifier behaves on the example data in the following plots. Do not skip the second plot! Take a moment to think about what it shows.
Do not change the code yet.
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.model_selection import train_test_split
# split data in train and test sets
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2)
dtree = DecisionTreeClassifier(max_depth=3)
dtree.fit(X_train, Y_train)
dtree_y_pred = dtree.predict(X_train)
plot_tree(dtree)
plt.show()
# Plot the Prediction Behaviour of the Decision Tree
xx, yy = np.meshgrid(np.arange(-0.25, 1.25, 0.001),
np.arange(-0.25, 1.25, 0.001))
Z = dtree.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.4, cmap=plt.cm.RdYlBu)
plt.scatter(X_test[Y_test == -1][:, 0], X_test[Y_test == -1][:, 1], s=10, c="Red")
plt.scatter(X_test[Y_test == 1][:, 0], X_test[Y_test == 1][:, 1], s=10, c="Blue")
plt.plot([-1, 2], [-1, 2], c="Gray")
plt.xlabel('x1')
plt.ylabel('x2')
plt.xlim(-0.25, 1.25)
plt.ylim(-0.25, 1.25)
plt.title('Decision Tree Prediction Behaviour')
plt.legend([
"Noisy Test Points of Class -1",
"Noisy Test Points of Class 1",
"Best Classification Border"
])
plt.show()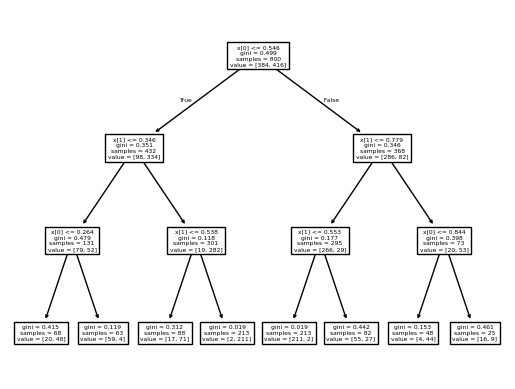
from sklearn.metrics import zero_one_loss
dtree_y_pred_train = dtree.predict(X_train)
dtree_y_pred_test = dtree.predict(X_test)
print("Train loss:", zero_one_loss(Y_train, dtree_y_pred_train))
print("Test loss:", zero_one_loss(Y_test, dtree_y_pred_test))Train loss: 0.10624999999999996
Test loss: 0.15000000000000002
The max_depth Parameter¶
Your answer
Now temper with the code above to check your answers.
The second code cell shows the 0-1 loss of the decision tree model on the training and test data separately.
Make sure to run the whole notebook multiple times to get results on different data! Especially in the tasks of the next section, it might be the case that your results are simply not positive by chance.
Over- and Underfitting¶
Your answer
4.
5.
6.
On the Leaf Level¶
Your answer
2.
3.
4.
Random Forests¶
See how random forests hold up in a comprehensive current benchmark on tabular data called >>TabArena<< (Published 2025 at NeurIPS).